概率论与数理统计基础概念与重要定义汇总_概率论与数理统计博客-程序员宅基地
技术标签: 夏令营 统计学 科研之路:Mobile+AI+game theory 概率论
一、随机事件和概率
1:互斥,对立,独立事件的定义和性质。
互斥事件 \color{red}\textbf{互斥事件} 互斥事件
事件A和B的交集为空,A与B就是互斥事件,也叫互不相容事件。也可叙述为:不可能同时发生的事件。如A∩B为不可能事件(A∩B=Φ),那么称事件A与事件B互斥,其含义是:事件A与事件B在任何一次试验中不会同时发生。
则P(A+B)=P(A)+P(B)(这个公式何时成立在我一面thu叉院的时候被问到过,我神tm就答了一个相互独立/(ㄒoㄒ)/~~)且P(A)+P(B)≤1
对立事件 \color{red}\textbf{对立事件} 对立事件
若A交B为不可能事件,A并B为必然事件,那么称A事件与事件B互为对立事件,其含义是:事件A和事件B必有一个且仅有一个发生。
对立事件概率之间的关系:P(A)+P(B)=1。例如,在掷骰子试验中,A={出现的点数为偶数},b={出现的点数为奇数},A∩B为不可能事件,A∪B为必然事件,所以A与B互为对立事件。
互斥事件与对立事件两者的联系在于:对立事件属于一种特殊的互斥事件。
它们的区别可以通过定义看出来:一个事件本身与其对立事件的并集等于总的样本空间;而若两个事件互为互斥事件,表明一者发生则另一者必然不发生,但不强调它们的并集是整个样本空间。即对立必然互斥,互斥不一定会对立。
独立事件 \color{red}\textbf{独立事件} 独立事件
设A,B是试验E的两个事件,若 P ( A ) > 0 P(A)>0 P(A)>0,可以定义 P ( B ∣ A ) P(B∣A) P(B∣A).一般A的发生对B发生的概率是有影响的,所以条件概率 P ( B ∣ A ) ≠ P ( B ) P(B∣A)≠P(B) P(B∣A)=P(B),而只有当A的发生对B发生的概率没有影响的时候(即A与B相互独立)才有条件概率 P ( B ∣ A ) = P ( B ) P(B∣A)=P(B) P(B∣A)=P(B).这时,由乘法定理 P ( A ∩ B ) = P ( B ∣ A ) P ( A ) = P ( A ) P ( B ) . P(A∩B)=P(B∣A)P(A)=P(A)P(B). P(A∩B)=P(B∣A)P(A)=P(A)P(B).
定义:设A,B是两事件,如果满足等式 P ( A ∩ B ) = P ( A B ) = P ( A ) P ( B ) P(A∩B)=P(AB)=P(A)P(B) P(A∩B)=P(AB)=P(A)P(B),则称事件A,B相互独立,简称A,B独立.
容易推广:设A,B,C是三个事件,如果满足 P ( A B ) = P ( A ) P ( B ) P(AB)=P(A)P(B) P(AB)=P(A)P(B), P ( B C ) = P ( B ) P ( C ) P(BC)=P(B)P(C) P(BC)=P(B)P(C), P ( A C ) = P ( A ) P ( C ) P(AC)=P(A)P(C) P(AC)=P(A)P(C), P ( A B C ) = P ( A ) P ( B ) P ( C ) P(ABC)=P(A)P(B)P(C) P(ABC)=P(A)P(B)P(C),则称事件A,B,C相互独立
更一般的定义是, A 1 , A 2 , … … , A n A1,A2,……,An A1,A2,……,An是 n ( n ≥ 2 ) n(n≥2) n(n≥2)个事件,如果对于其中任意2个,任意3个,…任意n个事件的积事件的概率,都等于各个事件概率之积,则称事件 A 1 , A 2 , … , A n A1,A2,…,An A1,A2,…,An相互独立
2:概率,条件概率和五大概率公式
概率公理与条件概率 \color{red}\textbf{概率公理与条件概率} 概率公理与条件概率
什么是概率?设实验E的样本空间为 Ω \Omega Ω,则称实值函数 P P P为概率,如果 P P P满足下列三个条件
- 对于任意事件A,满足 P ( A ) ≥ 0 P(A)\geq0 P(A)≥0
- 对于必然事件 Ω \Omega Ω有 P ( A ) = 1 P(A)=1 P(A)=1
- 对于两两互斥的可数无穷个事件 A 1 , A 2 , . . . , A N . . . A_1,A_2,...,A_N... A1,A2,...,AN...,有
P ( A 1 ∪ A 2 ∪ . . . ∪ A N ∪ . . . ) = P ( A 1 ) + P ( A 2 ) + . . . + P ( A N ) + . . . P(A_1\cup A_2\cup...\cup A_N\cup...)=P(A_1)+P(A_2)+...+P(A_N)+... P(A1∪A2∪...∪AN∪...)=P(A1)+P(A2)+...+P(AN)+...
什么是条件概率?设 A , B A,B A,B为两个事件,且 P ( A ) > 0 P(A)>0 P(A)>0,称
P ( B ∣ A ) = P ( A B ) P ( A ) P(B|A)=\frac{P(AB)}{P(A)} P(B∣A)=P(A)P(AB)
为在事件A发生的条件下事件B发生的条件概率。
五大概率公式 \color{red}\textbf{五大概率公式} 五大概率公式
- 加法公式: P ( A ∪ B ) = P ( A ) + P ( B ) − P ( A B ) P(A\cup B)=P(A)+P(B)-P(AB) P(A∪B)=P(A)+P(B)−P(AB),P(A∪B∪C)=P(A)+P(B)+P-P(AB)-P(BC)-P(AC)+P(ABC).
- 减法公式: P ( A − B ) = P ( A ) − P ( A B ) P(A-B)=P(A)-P(AB) P(A−B)=P(A)−P(AB)
- 乘法公式:当 P ( A ) > 0 P(A)>0 P(A)>0时, P ( A B ) = P ( A ) P ( B ∣ A ) P(AB)=P(A)P(B|A) P(AB)=P(A)P(B∣A)
- 全概率公式:设 B 1 , B 2 , . . . , B n B_1,B_2,...,B_n B1,B2,...,Bn为样本区间内概率均不为零的一个完备事件组,则对任意事件 A A A,有 P ( A ) = ∑ i = 1 n P ( B i ) P ( A ∣ B i ) P(A)=\sum_{i=1}^n P(B_i)P(A|B_i) P(A)=∑i=1nP(Bi)P(A∣Bi)。
- 贝叶斯公式:设 B 1 , B 2 , . . . , B n B_1,B_2,...,B_n B1,B2,...,Bn为样本区间内概率均不为零的一个完备事件组,则对任意事件 A A A且 P ( A ) > 0 P(A)>0 P(A)>0,有
P ( B j ∣ A ) = P ( B j ) P ( A ) P ( A ) = P ( B j ) P ( A ∣ B j ) ∑ i = 1 n P ( B i ) P ( A ∣ B i ) P(B_j|A)=\frac{P(B_j)P(A)}{P(A)}=\frac{P(B_j)P(A|B_j)}{\sum_{i=1}^nP(B_i)P(A|B_i)} P(Bj∣A)=P(A)P(Bj)P(A)=∑i=1nP(Bi)P(A∣Bi)P(Bj)P(A∣Bj)
3:古典型,几何型概率和伯努利试验
古典型-能通过样本点数出来的概率 \color{red}\textbf{古典型-能通过样本点数出来的概率} 古典型-能通过样本点数出来的概率

几何型:通过几何度量计算的概率 \color{red}\textbf{几何型:通过几何度量计算的概率} 几何型:通过几何度量计算的概率

伯努利试验:独立重复实验 \color{red}\textbf{伯努利试验:独立重复实验} 伯努利试验:独立重复实验
伯努利试验(Bernoulli experiment)是在同样的条件下重复地、相互独立地进行的一种随机试验,其特点是该随机试验只有两种可能结果:发生或者不发生。我们假设该项试验独立重复地进行了n次,那么就称这一系列重复独立的随机试验为n重伯努利试验,或称为伯努利概型。单个伯努利试验是没有多大意义的,然而,当我们反复进行伯努利试验,去观察这些试验有多少是成功的,多少是失败的,事情就变得有意义了,这些累计记录包含了很多潜在的非常有用的信息。
4:易错问题汇总
- P ( A ∪ B ) = 1 P(A\cup B)=1 P(A∪B)=1不能推出 A ∪ B = Ω A\cup B=\Omega A∪B=Ω,同样 P ( A B ) = 0 P(AB)=0 P(AB)=0也不能推出 A B = ∅ AB=\emptyset AB=∅。这两个关系只能从右往左推,仅给出概率是得不到事件的结论的。
二、随机变量及其分布
1:随机变量及其分布函数
随机变量 \color{red}\textbf{随机变量} 随机变量
在样本空间 Ω \Omega Ω上的实值函数 X = X ( ω ) , ω ∈ Ω X=X(\omega),\omega\in\Omega X=X(ω),ω∈Ω称为随机变量,简记为 X X X。随机变量不是一个变量,而是实值函数。
分布函数 \color{red}\textbf{分布函数} 分布函数
分布函数(英文Cumulative Distribution Function, 简称CDF),是概率统计中重要的函数,正是通过它,可用数学分析的方法来研究随机变量。分布函数是随机变量最重要的概率特征,分布函数可以完整地描述随机变量的统计规律,并且决定随机变量的一切其他概率特征。
分布函数 F ( x ) F(x) F(x)是定义在 ( − ∞ , ∞ ) (-\infty,\infty) (−∞,∞)上的一个实值函数, F ( x ) F(x) F(x)的值等于随机变量 X X X在区间 ( − ∞ , x ] (-\infty,x] (−∞,x]上取值的概率,即事件 X ≤ x X\leq x X≤x的概率:
F ( x ) = P ( X ≤ x ) , x ∈ ( − ∞ , ∞ ) \color{blue}F(x)=P(X\leq x),x\in (-\infty,\infty) F(x)=P(X≤x),x∈(−∞,∞)
分布函数的性质主要有三条,单调不减,负无穷收敛到0 lim x → + ∞ F ( x ) = 1 \lim_{x\rightarrow+\infty} F(x)=1 limx→+∞F(x)=1,正无穷收敛到1。右连续性 F ( x + 0 ) = F ( x ) F(x+0)=F(x) F(x+0)=F(x).
这三个条件同样是 F ( x ) F(x) F(x)成为某一随机变量的分布函数的充分必要条件。
分布函数的定义对于离散型随机变量和连续型随机变量都是一致的,但是对于连续型随机变量而言,他还有概率密度
把随机变量的概率分布表推广到无限情况,就可以得到连续型随机变量的概率密度函数。 此时,随机变量取每个具体的值的概率为0,但在落在每一点处的概率是有相对大小的,描述这个概念的,就是概率密度函数。 你可以把这个想象成一个实心物体,在每一点处质量为0,但是有密度,即有相对质量大小,他有以下两条主要的性质。
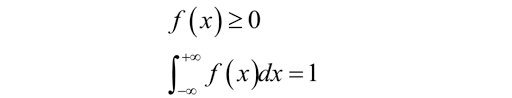
2:常用分布
伯努利分布(0-1分布) \color{red}\textbf{伯努利分布(0-1分布)} 伯努利分布(0-1分布)
0 — 1 0—1 0—1分布就是 n = 1 n=1 n=1情况下的二项分布。即只先进行一次事件试验,该事件发生的概率为 p p p,不发生的概率为 1 − p 1-p 1−p。这是一个最简单的分布,任何一个只有两种结果的随机现象都服从 0 − 1 0-1 0−1分布。
二项分布 \color{red}\textbf{二项分布} 二项分布
一般地,如果随机变量 X X X有分布律

则称 X X X服从参数为 n n n和 p p p的二项分布,我们记为 X ∼ B ( n , p ) X\thicksim B(n,p) X∼B(n,p)或 X ∼ b ( n , p ) X\thicksim b(n,p) X∼b(n,p)。
含义:在 n n n次独立重复的伯努利试验中,若每次实验的成功率为 p p p,则在 n n n次独立重复实验种成功的总次数 X X X服从二项分布。当 n = 1 n=1 n=1时,二项分布退化为 0 − 1 0-1 0−1分布。
几何分布 \color{red}\textbf{几何分布} 几何分布
如果随机变量 X X X的分布律为:

则称 X X X服从参数为 p p p的几何分布。
含义:在 n n n次伯努利试验中,试验 k k k次才得到第一次成功的机率服从几何分布
超几何分布 \color{red}\textbf{超几何分布} 超几何分布
如果随机变量 X X X的分布律为:

则称 X X X服从参数为 n , N , M n,N,M n,N,M的超几何分布。
含义:如果 N N N件产品中含有 M M M件次品,从中任意一次取出 n n n件(不放回依次取出 n n n件),另 X X X=抽取的 n n n件产品中的次品件数,则 X X X服从参数为 n , N , M n,N,M n,N,M的超几何分布。
如果有放回的取 n n n次,那么服从 B ( N , M N ) B(N,\frac{M}{N}) B(N,NM)。
泊松分布 \color{red}\textbf{泊松分布} 泊松分布
如果随机变量 X X X的分布律为:

则称 X X X服从参数为 λ \lambda λ的泊松分布,记为 X ∼ P ( λ ) X\thicksim P(\lambda) X∼P(λ)。
泊松分布的参数λ是单位时间(或单位面积)内随机事件的平均发生次数。 泊松分布适合于描述单位时间内随机事件发生的次数。
在实际事例中,当一个随机事件,例如某电话交换台收到的呼叫、来到某公共汽车站的乘客、某放射性物质发射出的粒子、显微镜下某区域中的白血球等等,以固定的平均瞬时速率 λ λ λ(或称密度)随机且独立地出现时,那么这个事件在单位时间(面积或体积)内出现的次数或个数就近似地服从泊松分布 P ( λ ) P(λ) P(λ)。
指数分布 \color{red}\textbf{指数分布} 指数分布
连续型均匀分布:如果连续型随机变量 X X X具有如下的概率密度函数,
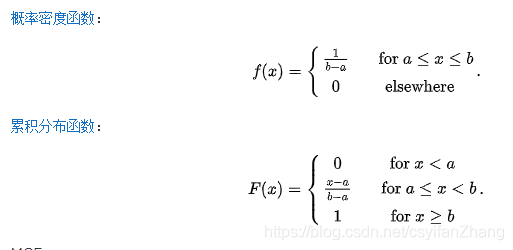
则称 X X X服从 [ a , b ] [a,b] [a,b]上的均匀分布(uniform distribution),记为 X ∼ U ( a , b ) X\thicksim U(a,b) X∼U(a,b)。
正态分布 \color{red}\textbf{正态分布} 正态分布
如果随机变量 X X X的概率密度为:

其中 μ , σ \mu,\sigma μ,σ为常数而且 σ > 0 \sigma>0 σ>0,则称 X X X服从参数为 μ , σ \mu,\sigma μ,σ的正态分布,记作 X ∼ N ( μ , σ 2 ) X\thicksim N(\mu,\sigma^2) X∼N(μ,σ2)。当 μ = 0 , σ 2 = 1 \mu=0,\sigma^2=1 μ=0,σ2=1时,称 X X X服从标准正态分布。
三、多维随机变量及其分布
1-二维随机变量及其分布
二维随机变量 \color{red}\textbf{二维随机变量} 二维随机变量
设 X = X ( = ω ) X=X(=\omega) X=X(=ω), Y = Y ( ω ) Y=Y(\omega) Y=Y(ω)是定义在样本空间 Ω \Omega Ω上的两个随机变量,则称向量 ( X , Y ) (X,Y) (X,Y)为二维随机变量或者随机向量。
二维随机变量的分布 \color{red}\textbf{二维随机变量的分布} 二维随机变量的分布
F ( x , y ) = P ( X ≤ x , Y ≤ y ) F(x,y)=P(X\leq x,Y\leq y) F(x,y)=P(X≤x,Y≤y),该分布具有如下的性质
- 对任意的 x , y x,y x,y, 0 ≤ F ( x , y ) ≤ 1 0\leq F(x,y)\leq 1 0≤F(x,y)≤1
- F ( − ∞ , y ) = F ( x , − ∞ ) = F ( − ∞ , − ∞ ) = 0 , F ( + ∞ , + ∞ ) = 1 F(-\infty,y)=F(x,-\infty)=F(-\infty,-\infty)=0,F(+\infty,+\infty)=1 F(−∞,y)=F(x,−∞)=F(−∞,−∞)=0,F(+∞,+∞)=1
- F ( x , y ) F(x,y) F(x,y)关于 x , y x,y x,y均单调不减而且右连续。
- P ( a < X ≤ b , c < Y ≤ d ) = F ( b , d ) − F ( b , c ) − F ( a , d ) + F ( a , c ) P(a<X\leq b,c<Y\leq d)=F(b,d)-F(b,c)-F(a,d)+F(a,c) P(a<X≤b,c<Y≤d)=F(b,d)−F(b,c)−F(a,d)+F(a,c)
二维随机变量的边缘分布 \color{red}\textbf{二维随机变量的边缘分布} 二维随机变量的边缘分布
设二维随机变量 ( X , Y ) (X,Y) (X,Y)的分布函数如上,那么称 F X ( x ) = P ( X ≤ x ) , F Y ( y ) = P ( Y ≤ y ) F_X(x)=P(X\leq x),F_Y(y)=P(Y\leq y) FX(x)=P(X≤x),FY(y)=P(Y≤y)为 ( X , Y ) (X,Y) (X,Y)关于 X X X和关于 Y Y Y的边缘分布函数。
边缘分布与二维随机变量分布函数的关系为:
F X ( x ) = P ( X ≤ x ) = P ( X ≤ x , Y < + ∞ ) = F ( x , + ∞ ) F_X(x)=P(X\leq x)=P(X\leq x,Y<+\infty)=F(x,+\infty) FX(x)=P(X≤x)=P(X≤x,Y<+∞)=F(x,+∞)
二维连续型随机变量的概率密度 \color{red}\textbf{二维连续型随机变量的概率密度} 二维连续型随机变量的概率密度

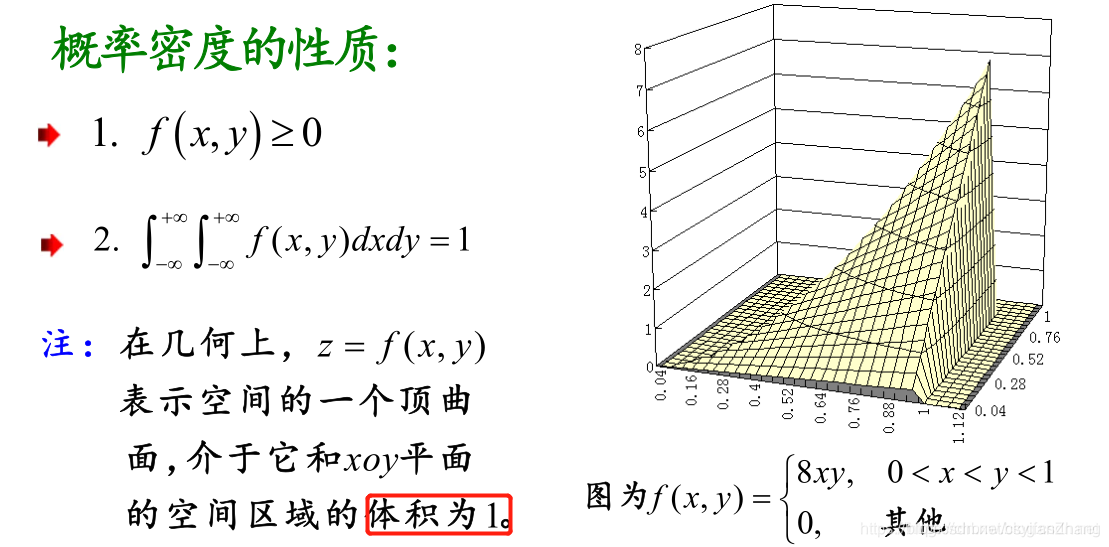

2-随机变量的独立性
如果对于任意 x , y x,y x,y,都有
P ( X ≤ x , Y ≤ y ) = P { X ≤ x } P { Y ≤ y } P(X\leq x,Y\leq y)=P\{X\leq x\}P\{Y\leq y\} P(X≤x,Y≤y)=P{
X≤x}P{
Y≤y}
即 F ( x , y ) = F X ( x ) F Y ( y ) F(x,y)=F_X(x)F_Y(y) F(x,y)=FX(x)FY(y),则称随机变量 X X X与 Y Y Y相互独立。
随机变量相互独立的充要条件 \color{red}\textbf{随机变量相互独立的充要条件} 随机变量相互独立的充要条件
- 离散型随机变量 X X X和 Y Y Y相互独立的充要条件:对任意 i , j = 1 , 2 , . . , i,j=1,2,.., i,j=1,2,..,有 P { X = x i , Y = y i } = P { X = x i } P { Y = y i } P\{X=x_i,Y=y_i\}=P\{X=x_i\}P\{Y=y_i\} P{ X=xi,Y=yi}=P{ X=xi}P{ Y=yi},即 p i j = p i p j p_{ij}=p_ip_j pij=pipj
- 连续型随机变量 X X X, Y Y Y相互独立的充要条件:对于任意的 x , y x,y x,y,有 f ( x , y ) = f X ( x ) f Y ( y ) f(x,y)=f_X(x)f_Y(y) f(x,y)=fX(x)fY(y)。可将两个随机变量的独立性推广到两个以上随机变量的情形。
3-两个随机变量 Z = g ( X , Y ) Z=g(X,Y) Z=g(X,Y)的分布
当 X , Y X,Y X,Y为离散型随机变量时, Z Z Z的分布律与一维离散型类似。
当 X , Y X,Y X,Y为连续型随机变量时, F Z ( z ) F_Z(z) FZ(z)的求法,可以用公式
F Z ( z ) = P ( Z ≤ z ) = P { g ( X , Y ) ≤ z } = ∫ ∫ g ( X , Y ) ≤ z f ( x , y ) d x d y F_Z(z)=P(Z\leq z)=P\{g(X,Y)\leq z\}=\int\int_{g(X,Y)\leq z} f(x,y)dxdy FZ(z)=P(Z≤z)=P{ g(X,Y)≤z}=∫∫g(X,Y)≤zf(x,y)dxdy
四、随机变量的数字特征
1:随机变量的数学期望
数学期望 \textbf{数学期望} 数学期望
- 离散型随机变量:设随机变量 X X X的概率分布为 P { X = x k } = p k P\{X=x_k\}=p_k P{
X=xk}=pk,如果级数 ∑ k = 1 ∞ x k p k \color{red}\sum_{k=1}^\infty x_kp_k ∑k=1∞xkpk绝对收敛,则称此级数为随机变量 X X X的数学期望或均值,记作 E ( X ) E(X) E(X)。
连续型随机变量, f ( x ) f(x) f(x)为随机变量 X X X的概率密度,那么他的数学期望为 ∫ − ∞ + ∞ x f ( x ) d x \color{red}\int_{-\infty}^{+\infty} xf(x)dx ∫−∞+∞xf(x)dx
数学期望的性质 \textbf{数学期望的性质} 数学期望的性质
- 设C是常数,X是随机变量,那么 E ( C ) = C E(C)=C E(C)=C, E ( C X ) = C E ( X ) E(CX)=CE(X) E(CX)=CE(X)
- 设 X , Y X,Y X,Y是任意两个随机变量,那么 E ( X + Y ) = E ( X ) + E ( Y ) E(X+Y)=E(X)+E(Y) E(X+Y)=E(X)+E(Y)。
- 设 X , Y X,Y X,Y是任意两个随机变量,那么 E ( X Y ) = E ( X ) E ( Y ) E(XY)=E(X)E(Y) E(XY)=E(X)E(Y)当且仅当二者不相关。
随机变量X的函数Y=g(X)的数学期望 \textbf{随机变量X的函数Y=g(X)的数学期望} 随机变量X的函数Y=g(X)的数学期望
建议看一篇好文:https://www.cnblogs.com/bigmonkey/p/11088669.html
- 离散性随机变量: E ( g ( X ) ) = ∑ i = 1 ∞ g ( x i ) p i \color{red}E(g(X))=\sum_{i=1}^\infty g(x_i)p_i E(g(X))=∑i=1∞g(xi)pi, p i p_i pi是 x i x_i xi出现的概率
- 连续型随机变量: E ( g ( X ) ) = ∫ − ∞ + ∞ g ( x ) f ( x ) d x \color{red}E(g(X))=\int_{-\infty}^{+\infty} g(x)f(x)dx E(g(X))=∫−∞+∞g(x)f(x)dx, f ( X ) f(X) f(X)是 X X X的概率密度。
随机变量(X,Y)的函数Z=g(X,Y)的数学期望 \textbf{随机变量(X,Y)的函数Z=g(X,Y)的数学期望} 随机变量(X,Y)的函数Z=g(X,Y)的数学期望
- 离散性随机变量: E ( g ( X , Y ) ) = ∑ i = 1 ∞ ∑ j = 1 ∞ p i , j g ( x i , y j ) \color{red}E(g(X,Y))=\sum_{i=1}^\infty\sum_{j=1}^\infty p_{i,j}g(x_i,y_j) E(g(X,Y))=∑i=1∞∑j=1∞pi,jg(xi,yj),其中 p i , j = P ( X = x i , Y = y j ) p_{i,j}=P(X=x_i,Y=y_j) pi,j=P(X=xi,Y=yj)。
- 连续型随机变量: E ( g ( X , Y ) ) = ∫ − ∞ + ∞ ∫ − ∞ + ∞ g ( x , y ) f ( x , y ) d x d y \color{red}E(g(X,Y))=\int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty}g(x,y)f(x,y)dxdy E(g(X,Y))=∫−∞+∞∫−∞+∞g(x,y)f(x,y)dxdy, f ( X , Y ) f(X,Y) f(X,Y)是 Z Z Z的概率密度。
2:随机变量的方差
- 随机变量 X X X的方差定义为 D ( X ) = E { [ X − E ( X ) ] 2 } D(X)=E\{[X-E(X)]^2\} D(X)=E{ [X−E(X)]2}
- 方差计算公式: D ( X ) = E ( X 2 ) − [ E ( X ) ] 2 D(X)=E(X^2)-[E(X)]^2 D(X)=E(X2)−[E(X)]2
- 方差的性质:(1)常数的方差为0.(2) D ( a X + b ) = a 2 D ( X ) D(aX+b)=a^2D(X) D(aX+b)=a2D(X)。(3) D ( X + Y ) = D ( X ) + D ( Y ) D(X+Y)=D(X)+D(Y) D(X+Y)=D(X)+D(Y)成立的充要条件是 X , Y X,Y X,Y不相关。
3:常用随机变量的数学期望和方差

4:矩、协方差和相关系数
这里需要注意的是两个随机变量不相关,这是区别于独立,互斥的另一种关系,不相关的充要条件是两个随机变量的相关系数 ρ X Y = 0 \rho_{XY}=0 ρXY=0。如果两个变量独立,那么相关系数一定为0,但是相关系数为0是线性不相关,不能推出两变量相互独立。
五、理解大数定律和中心极限定律
1:大数定律和中心极限定理的区别和联系
这里主要是理解,我就不摆公式了,
在统计活动中,人们发现,在相同条件下大量重复进行一种随机实验时,一件事情发生的次数与实验次数的比值,即该事件发生的频率值会趋近于某一数值。重复次数多了,这个结论越来越明显。这个就是最早的大数定律。一般大数定律讨论的是n个随机变量平均值的稳定性。
而中心极限定理则是证明了在很一般的条件下,n个随即变量的和当n趋近于正无穷时的极限分布是正态分布。(对,就是它,跟我念,正态分布!O.O哎,哪里都有它,记住记住。)
一句话解释:大数定律讲的是样本均值收敛到总体均值,说白了就是期望,如图一样:
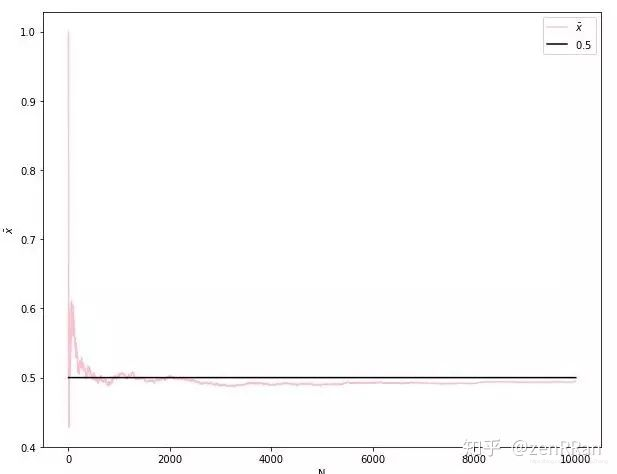
而中心极限定理告诉我们,当样本足够大时,样本均值的分布会慢慢变成正态分布,对,就是如图这个样子:

上面是区别,那么联系根据区别也能看出来,都总结的是在独立同分布条件下的随即变量平均值的表现。
2:简单总结他们的作用
我们假设有n个独立随机变量,令他们的和为:
S n = ∑ i = 1 n X i S_n=\sum_{i=1}^n X_i Sn=i=1∑nXi
那么大数定律(以一般的大数定律为例),它的公式为:
S n n − E ( X ) → 0 \frac{S_n}{n}-E(X)\rightarrow 0 nSn−E(X)→0
而中心极限定理的公式为:
n ( S n n − E ( X ) ) → N ( 0 , ∑ ) \sqrt{n}(\frac{S_n}{n}-E(X))\rightarrow N(0,\sum) n(nSn−E(X))→N(0,∑)
注意:上面两个公式,一个是值为0,一直均值为0的正太分布;而左边极为相似!但不一样的。第二个公式比第一个公式多了 n \sqrt n n,所以你就记住这条就不会混乱了,来,跟我念一遍:“差了个 n \sqrt n n!”
六、参数估计
1:点估计
总体分布的参数在很多情况下是未知的,如均值 μ μ μ、方差 σ 2 \sigma^2 σ2、泊松分布的 λ λ λ、二项分布的比例 π π π,其它分布还会有更多的未知参数,需要通过样本进行相应的估计,这种估计值就是点估计。
点估计的评价:
无偏性:如果参数估计值的数学期望等于被估计的参数值 E ( θ ) ^ E(\theta\widehat) E(θ) ,则称此估计量为无偏估计。与此相反则称为有偏估计。
有效性:当一个参数有多个无偏估计时,估计方差越小则越有效。
相合性(一致性):如果随着样本量增大,参数的估计量趋于被估计的参数值。
2:矩估计
矩估计,即矩估计法,也称“矩法估计”,就是利用样本矩来估计总体中相应的参数。首先推导涉及感兴趣的参数的总体矩(即所考虑的随机变量的幂的期望值)的方程。然后取出一个样本并从这个样本估计总体矩。接着使用样本矩取代(未知的)总体矩,解出感兴趣的参数。从而得到那些参数的估计。
矩法估计原理简单、使用方便,使用时可以不知总体的分布,而且具有一定的优良性质(如矩估计为Eξ的一致最小方差无偏估计)。矩法估计量实际上只集中了总体的部分信息,这样它在体现总体分布特征上往往性质较差,只有在样本容量n较大时,才能保障它的优良性,因而理论上讲,矩法估计是以大样本为应用对象的。
用样本矩作为相应的总体矩估计来求出估计量的方法.其思想是:如果总体中有 K K K个未知参数,可以用前 K K K阶样本矩估计相应的前 K K K阶总体矩,然后利用未知参数与总体矩的函数关系,求出参数的估计量。即有多少未知参数,就利用矩列几个方程。
令样本的 l l l阶原点矩为 A l = 1 n ∑ i = 1 n X i l A_l=\frac{1}{n}\sum_{i=1}^n X_i^l Al=n1∑i=1nXil,而每阶矩肯定也是 X X X分布中未知参数 θ 1 , θ 2 , . . . , θ n \theta_1,\theta_2,...,\theta_n θ1,θ2,...,θn的函数,即
α l ( θ 1 , θ 2 , . . . , θ n ) = A l , l = 1 , 2 , . . . , k \alpha_l(\theta_1,\theta_2,...,\theta_n)=A_l,l=1,2,...,k αl(θ1,θ2,...,θn)=Al,l=1,2,...,k
3:最大似然估计
极大似然估计,通俗理解来说,就是利用已知的样本结果信息,反推最具有可能(最大概率)导致这些样本结果出现的模型参数值!

最大似然估计,只是一种概率论在统计学的应用,它是参数估计的方法之一。说的是已知某个随机样本满足某种概率分布,但是其中具体的参数不清楚,参数估计就是通过若干次试验,观察其结果,利用结果推出参数的大概值。最大似然估计是建立在这样的思想上:已知某个参数能使这个样本出现的概率最大,我们当然不会再去选择其他小概率的样本,所以干脆就把这个参数作为估计的真实值。
求最大似然函数估计值的一般步骤:
(1) 写出似然函数
(2) 对似然函数取对数,并整理
(3) 求导数
(4) 解似然方程
智能推荐
计算机的外围设备简介_计算机外围固定-程序员宅基地
文章浏览阅读6.1k次,点赞3次,收藏5次。外围设备介绍计算机的外围设备(简称外设)虽然很多,但按功能分大类只有四类:输入、输出、存储、网络通讯。有些专业计算机需要的外围设备也不尽相同,并不都需要这四类外围设备。外围设备可以按需要组装,有些专业计算机甚至可以将存储设备和主芯片集成到一片芯片上,从而不再需要外加存储设备。最早的计算机(那时还只能称为计算器,只能做简单运算,如ABC机和ENIAC机)输入只是一些拨码开关,只能输入数字(还得是二进_计算机外围固定
java 图片中加文字_java怎么在图片上加文字-程序员宅基地
文章浏览阅读1.5k次。java 图片中加文字_java怎么在图片上加文字
GBase8cGDCA认证模拟题题库(三)_如果需要打开delete语句的审计功能,需要开启下面哪个参数-程序员宅基地
文章浏览阅读720次,点赞20次,收藏6次。B 选项,在创建模式时,可以不指定模式名。C 选项,兼容模式可选值为 AB、C、PG.安装GBase 8c分布式集群时所需的配置文件gbase.yml,在解压GBase8cV5 S3.0.0BXX CentOS x86 64.tar.bz2压缩包生成的目录中得到。真值的有效文本值是: TRUE、t、"true'、y、yes'、"1'TRUE'、true、整数范围内1~2^63-1、整数范围内-1~-2^63。GBase 8c 使用create table 创建表时,不指定参数,默认是astore,行存表。_如果需要打开delete语句的审计功能,需要开启下面哪个参数
xml文件中几个名词_xml文件里面的名词-程序员宅基地
文章浏览阅读334次。1 xmlns是XML Namespaces的缩写,中文名称是XML(标准通用标记语言的子集)命名空间。 web-app是web.xml的根节点标签名称 version是版本的意思 xmlns是web.xml文件用到的命名空间 xmlns:xsi是指web.xml遵守xml规范 xsi:schemaLocation是指具体用到的schema资源_xml文件里面的名词
【OpenGL】中点圆、椭圆生成算法_用setpixel函数中点画圆算法代码c++-程序员宅基地
文章浏览阅读1.6w次,点赞12次,收藏69次。OpenGL 中点圆、椭圆生成算法_用setpixel函数中点画圆算法代码c++
HTML-CSS实现背景图片出现不同的位置_css背景图高度占据一半另一半有别的背景色-程序员宅基地
文章浏览阅读2.1k次。首先在HTML中写入div,命名为img,在这个div中加入一个span标签并命名为img-bg和img50(5星为50).<div class="img"> <span class="img-bg img50"></span> <span class="img-bg img45"></span> <span class="img-bg img40"></span> </div> 在css代码._css背景图高度占据一半另一半有别的背景色
随便推点
duilib vs2015 安装_DuiLib(1)——简单的win32窗口-程序员宅基地
文章浏览阅读169次。资源下载https://yunpan.cn/cqF6icWRN5CTc 访问密码 92e3 注:DUILIB库.7z 是vs2015下编译好的动态库及静态库,如上图所示一、新建一个win32工程项目设置中选择:debug,常规中:全程无优化-全程无优化,多线程调试 (/MTd);我的项目选择的是静态编译,使用的是静态库,就不需要带duilib.dll文件了代码如下:#include #inclu..._vs2015使用duilib
OpenGL: 渲染管线理论详解_通过此次实验你对固定渲染管线的opengl编程有什么了解。-程序员宅基地
文章浏览阅读5k次,点赞4次,收藏13次。学习着色器,并理解着色器的工作机制,就要对OpenGL的固定功能管线有深入的了解。首先要知道几个OpenGL的术语:渲染(rendering):计算机根据模型(model)创建图像的过程。模型(model):根据几何图元创建的物体(object)。几何图元:包括点、直线和多边形等,它是通过顶点(vertex)指定的。 最终完成了渲染的图像是由在屏幕上绘制的像素组成的。在内存中,和像素有关的信息(如像素的颜色)组织成位平面的形式,位平面是一块内存区域,保存了屏幕上每个像素的一个位的信息。_通过此次实验你对固定渲染管线的opengl编程有什么了解。
Android MPAndroidChart:动态添加统计数据线【8】_android 动态统计-程序员宅基地
文章浏览阅读3.9k次。Android MPAndroidChart:动态添加统计数据线【8】本文在附录相关文章6的基础上,动态的依次增加若干条统计折线(相当于批量增加数据点)。布局文件:
vmware中的linux虚拟机如何增加磁盘容量_linux虚拟机磁盘空间不足-程序员宅基地
文章浏览阅读6.3k次。vmware中 centos的磁盘大小 20G->30G现象:fdisk -l可以看到增大后的磁盘总量,但是需要增加分区并格式化然后挂载才能使用.一、vmware中的设置先关闭虚拟机vm->settings->hard disk->utilities->expand->输入大小(增加后的大小)二、启动虚拟机,进入命令行1、 fdisk /dev/sda进入命令行Comman_linux虚拟机磁盘空间不足
Hadoop2.7.3下Mysql8.0下Hive2.3.8的安装_hive2.3.8安装-程序员宅基地
文章浏览阅读927次。hive安装前提:1.基于hadoop2.7的完全分布式集群搭建完成hadoop2.7集群搭建2.MySQL8.0安装完成 安装centos7上MySQL8.0Hive2.3.8的安装下载链接:https://mirrors.tuna.tsinghua.edu.cn/apache/下滑找到hive点击进去点击hive2.3.9(hive2.3.9和hive2.3.8差别不大)下载画红线的也就是bin.tar.gz后缀的hive解压安装下载完成后通过xftp传到虚拟机上(基操不在赘述)_hive2.3.8安装
The‘grub-efi-amd64-signed‘ package failed to install into /target/. Without the GRUB boot loader,_the grub-efiamd64-signed' package failed to instal-程序员宅基地
文章浏览阅读430次,点赞8次,收藏4次。在进行安装的时候有一个是否联网的选择,选择链接网络,则在安装的时候,可以看到在安装过程中,它会主动下载grub-efi-amd64-signed' package,确确实实,我在安装详情里看到了它有这个的download过程以及update过程。_the grub-efiamd64-signed' package failed to install intotarget without the g