欧拉法求解微分方程_欧拉法解微分方程-程序员宅基地
文章目录
欧拉法是一种求解微分方程的数值方法。微分方程的目标是求出方程的具体表达式,但数值方法则是根据方程求出其每一个点,而不是找出表达式,在工程上具有很大的实用性。
欧拉法求解微分方程组的原理
设有微分方程:
d x ( t ) d t = f ( x ) \frac{dx(t)}{dt} = f(x) dtdx(t)=f(x)
x ( t 0 ) = x 0 x(t_0)=x_0 x(t0)=x0已知。
我们对上述方程进行积分,积分区域为 [ t 0 , t 1 ] , Δ t = t 1 − t 0 [t_0,t_1],\Delta t = t_1-t_0 [t0,t1],Δt=t1−t0,可得:
x ( t 1 ) = x ( t 0 ) + ∫ t 0 t 1 f ( t ) d t x(t_1)=x(t_0)+\int_{t_0}^{t_1}f(t)dt x(t1)=x(t0)+∫t0t1f(t)dt
其中 x ( t 1 ) x(t_1) x(t1)就是我们要求解的东西了。于是,就差积分怎么解决了。
对于欧拉法来说,积分是靠梯形面积来近似,如下所示:
∫ t 0 t 1 f ( t ) d t = f ( x ( t 0 ) ) ( t 1 − t 0 ) = f ( x 0 ) Δ t \int_{t_0}^{t_1}f(t)dt = f(x(t_0))(t_1-t_0)=f(x_0)\Delta t ∫t0t1f(t)dt=f(x(t0))(t1−t0)=f(x0)Δt
带入上述方程即可得:
x ( t 1 ) = x ( t 0 ) + f ( x 0 ) Δ t x(t_1)=x(t_0)+f(x_0)\Delta t x(t1)=x(t0)+f(x0)Δt
按照上式进行递推,即可得:
x k + 1 = x k + f ( x k ) Δ t x_{k+1} = x_{k} + f(x_{k})\Delta t xk+1=xk+f(xk)Δt
其中 x 0 x_0 x0 已知。问题就搞定了。
*欧拉法原理图解
因为
f ( x k ) = d x d t ∣ t = t k f(x_k) = \frac{dx}{dt}|_{t=t_k} f(xk)=dtdx∣t=tk
所以递推式可以写成:
x k + 1 = x k + d x d t ∣ t = t k Δ t x_{k+1} = x_{k} + \frac{dx}{dt}|_{t=t_k}\Delta t xk+1=xk+dtdx∣t=tkΔt
而 d x d t \frac{dx}{dt} dtdx是所求方程 x ( t ) x(t) x(t)的斜率,因此实际上是将下图的阴影部分的面积来替代积分表达式:

欧拉法数值稳定性讨论
方便讨论,我们取一种简单情况,设有微分方程:
d x ( t ) d t = a x \frac{dx(t)}{dt} = ax dtdx(t)=ax
什么是数值稳定性问题?
假设 k 步计算中, x k x_k xk与实际值存在误差 ρ k \rho_k ρk,则第 k+1 步计算中,误差是否会增大。若是,则不稳定啦。因为越往后计算,这个误差肯定是越爆炸的。
那么欧拉法数值稳定性如何呢?首先假设 x k x_k xk与实际值存在误差 ρ k \rho_k ρk,根据递推公式:
x k + 1 = x k + f ( x k ) Δ t x_{k+1} = x_{k} + f(x_{k})\Delta t xk+1=xk+f(xk)Δt
设 f ( x k ) = a x k f(x_{k})=ax_{k} f(xk)=axk而:
x ^ k = x k + ρ k \hat{x}_k = x_k + \rho_{k} x^k=xk+ρk
故第 k+1 步时时:
x ^ k = ( 1 + a Δ t ) ( x k + ρ k ) = x k + 1 + ( 1 + a Δ t ) ρ k \hat{x}_k = (1+a\Delta t)(x_k+\rho_k)=x_{k+1}+(1+a\Delta t)\rho_k x^k=(1+aΔt)(xk+ρk)=xk+1+(1+aΔt)ρk
于是 k+1 步的误差为:
ρ k + 1 = ( 1 + a Δ t ) ρ k \rho_{k+1} = (1+a\Delta t)\rho_k ρk+1=(1+aΔt)ρk
若要求稳定,则必须有 ∣ 1 + a Δ t ∣ ≤ 1 |1+a\Delta t| \leq 1 ∣1+aΔt∣≤1
于是可得欧拉法的数值稳定区域如下:

欧拉法误差分析——局部截断误差
微分方程 d x d t = f ( x ) \frac{dx}{dt} = f(x) dtdx=f(x),用欧拉法时,我们的迭代方程是:
x k = x k − 1 + f ( x k − 1 ) Δ t = x k − 1 + d x d t ∣ t k − 1 Δ t x_{k} = x_{k-1} + f(x_{k-1})\Delta t =x_{k-1} + \frac{dx}{dt}|_{t_{k-1}}\Delta t xk=xk−1+f(xk−1)Δt=xk−1+dtdx∣tk−1Δt。
若对 x k x_{k} xk 进行泰勒展开,可得:
x ( t k ) = x ( t k − 1 + Δ t ) = x k − 1 + x ′ ( t k − 1 Δ t + x ′ ′ ( t k − 1 ) Δ t 2 + ⋯ x(t_{k}) = x(t_{k-1}+\Delta t) = x_{k-1} + x^{\prime}(t_{k-1} \Delta t + x^{\prime\prime}(t_{k-1}) \Delta t^2 + \cdots x(tk)=x(tk−1+Δt)=xk−1+x′(tk−1Δt+x′′(tk−1)Δt2+⋯
因此,欧拉法的截断误差为:
x ′ ′ ( t k − 1 ) Δ t 2 + ⋯ x^{\prime\prime}(t_{k-1}) \Delta t^2+ \cdots x′′(tk−1)Δt2+⋯
由于有 Δ t 2 \Delta t^2 Δt2,所以我称欧拉法的精度为 2-1 = 1 阶。
改进欧拉法原理
欧拉法是用梯形的面积来近似积分的,而且梯形的上底是用 KaTeX parse error: Expected 'EOF', got '}' at position 7: x_[i-1}̲时,曲线 x ( t ) x(t) x(t)的斜率来近似计算的,所以不太好,可以看到的是,欧拉法的精度只有一阶,其阶段误差与 Δ t 2 \Delta t^2 Δt2有关。这个误差之所以那么大,是因为我们在求积分(面积)的时候,用了以 x k − 1 x_{k-1} xk−1为上底的梯形去近似他。因此,我们需要对这个梯形的上底进行一定的修正。
首先,根据递推公式求出:
x k ( 0 ) = x k − 1 + f ( x k − 1 ) Δ t x_{k}^{(0)} = x_{k-1} + f(x_{k-1}) \Delta t xk(0)=xk−1+f(xk−1)Δt
之后再求出修正后的 x k x_{k} xk:
x k = x k − 1 + 1 2 ( f ( x k − 1 + x k ( 0 ) ) Δ t x_k = x_{k-1}+\frac{1}{2}(f(x_{k-1}+x_{k}^{(0)})\Delta t xk=xk−1+21(f(xk−1+xk(0))Δt
其原理图如下:
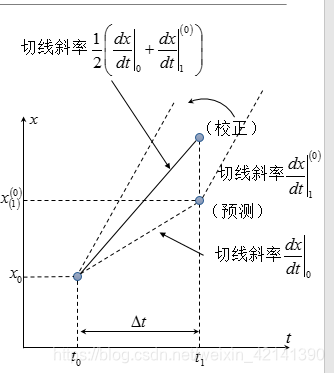
改进欧拉法的稳定性分析
设微分方程为 d x d t = λ x \frac{dx}{dt} = \lambda x dtdx=λx,于是KaTeX parse error: Undefined control sequence: \ambda at position 16: x_{k}^{(0)]=(1+\̲a̲m̲b̲d̲a̲\Delta t)x_{k-1…, f ( x k ( 0 ) = λ ( 1 + λ Δ t ) x k − 1 f(x_{k}^{(0)}=\lambda(1+\lambda\Delta t)x_{k-1} f(xk(0)=λ(1+λΔt)xk−1,于是 x k = ( 1 + λ Δ t + 1 2 ( λ Δ t ) 2 ) x k − 1 x_{k} = (1+\lambda\Delta t+\frac{1}{2}(\lambda\Delta t)^2)x_{k-1} xk=(1+λΔt+21(λΔt)2)xk−1
所以误差不增值的条件为: ∣ 1 + λ Δ t + 1 2 ( λ Δ t ) 2 ∣ ≤ 1 |1+\lambda\Delta t+\frac{1}{2}(\lambda\Delta t)^2|\leq1 ∣1+λΔt+21(λΔt)2∣≤1,表现在图上,即为:
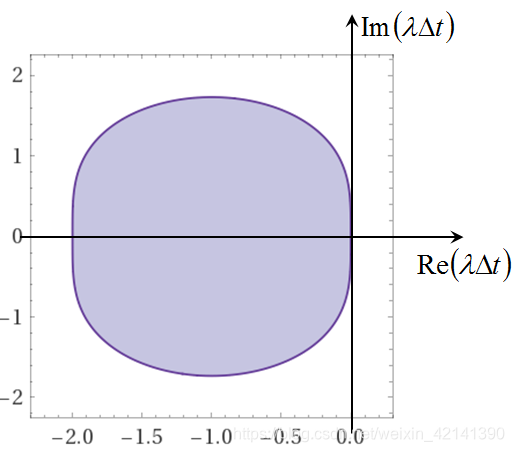
对比欧拉法,显然稳定区域大了一点。
改进欧拉法的误差分析
因为 f ( x k 0 ) = d x d t ∣ x k − 1 + d 2 x d t 2 ∣ x k − 1 Δ t 2 + O ( Δ t 2 ) f(x_{k}^{0}) = \frac{dx}{dt}|_{x_{k-1}}+\frac{d^{2}x}{dt^2}|_{x_{k-1}}\Delta t^2+O(\Delta t^2) f(xk0)=dtdx∣xk−1+dt2d2x∣xk−1Δt2+O(Δt2)
于是 x k = x k − 1 + d x d t ∣ x k − 1 Δ t + d 2 x d t 2 ∣ x k − 1 Δ t 2 x_{k} = x_{k-1}+\frac{dx}{dt}|_{x_{k-1}}\Delta t+\frac{d^2x}{dt^2}|_{x_{k-1}}\Delta t^2 xk=xk−1+dtdx∣xk−1Δt+dt2d2x∣xk−1Δt2
对比泰勒展开,可知其误差为 O ( Δ t 3 ) O(\Delta t^3) O(Δt3),因此精确度为 3-1 = 2阶!
隐式梯形法
隐式梯形法也是利用 x k x_k xk 来改善上底,只是其递推公式为:
x k = x k − 1 + Δ t 2 ( f ( x k − 1 ) + f ( x k ) ) x_{k} = x_{k-1} + \frac{\Delta t}{2}(f(x_{k-1})+f(x_{k})) xk=xk−1+2Δt(f(xk−1)+f(xk))
因此,上底的修正,包含在上述方程中。因此,不同于欧拉法,每一次迭代,隐式梯形法都要求解一次代数方程。
隐式梯形法的稳定性和误差
首先是稳定性,同样对于微分方程 d x d t = λ x \frac{dx}{dt}=\lambda x dtdx=λx,可得其误差的表达式为:
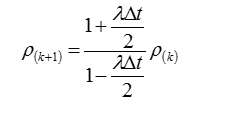
误差不增值条件: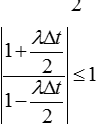
整理可得: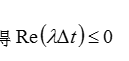
因此其稳定区域为:复平面的左半部分,可见比改进欧拉发、欧拉法要大得多!!
至于误差,同样可以证明的是隐式梯形法的精确度为2阶。
案例
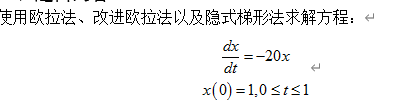
可见求解区域为 [0,1],我们设置求解的步数为 100,也即 Δ t = 0.01 s \Delta t = 0.01s Δt=0.01s,代码如下:
import numpy as np
import matplotlib.pyplot as plt
def f(x):
return -20*x
def uler(n,x0,t0,tn,f):
x = [x0]
t = [t0]
for i in range(n):
dt = (tn-t0)/n
tk = t[i]+dt
t.append(tk)
xk = x[i]+f(x[i])*dt
x.append(xk)
return x,t
def uler2(n,x0,t0,tn,f):
x = [x0]
t = [t0]
for i in range(n):
dt = (tn-t0)/n
tk = t[i]+dt
t.append(tk)
xkk = x[i]+f(x[i])*dt
xk = x[i]+ 1/2*(f(x[i])+f(xkk))*dt
x.append(xk)
return x,t
import sympy
x = sympy.symbols('x')
def uler3(n,x0,t0,tn,f):
x = [x0]
t = [t0]
for i in range(n):
dt = (tn-t0)/n
tk = t[i]+dt
t.append(tk)
xk = (x[i]+dt*f(x[i])/2)/(1+10*dt)
x.append(xk)
return x,t
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus'] = False
font1 = {
'family' : 'SimHei',
'weight' : 'normal',
'size' : 15,
}
def myplot(n,x0,t0,tn,f):
x1,t = uler(n,x0,t0,tn,f)
x2,t = uler2(n,x0,t0,tn,f)
plt.figure(figsize=(12,4))
plt.subplot(1,3,1)
plt.plot(t,x1,linewidth=3,color='r',label='欧拉法求解')
plt.xlabel('t',fontsize=24)
plt.ylabel('x',fontsize=24)
plt.legend(prop=font1)
plt.grid()
plt.subplot(1,3,2)
plt.plot(t,x2,linewidth=3,color='b',label='改进欧拉法求解')
plt.xlabel('t',fontsize=24)
plt.ylabel('x',fontsize=24)
plt.legend(prop=font1)
plt.grid()
x3,t = uler3(n,x0,t0,tn,f)
plt.subplot(1,3,3)
plt.plot(t,x3,linewidth=3,color='g',label='隐式梯形法求解')
plt.xlabel('t',fontsize=24)
plt.ylabel('x',fontsize=24)
plt.legend(prop=font1)
plt.grid()
if __name__ == '__main__':
myplot(100,1,0,1,f)
求解结果:
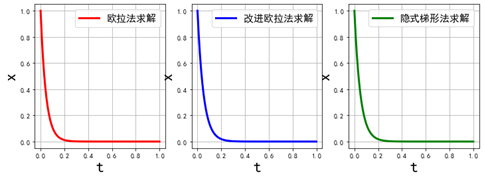
可以修改步长为 15,可得:
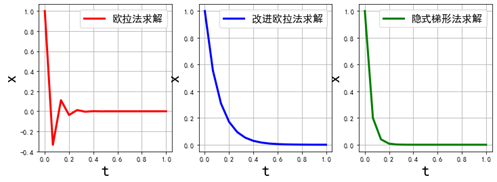
为什么步数为 15,结果就变形了呢?这是因为算法的稳定性、误差的原因,这里不再分析。
智能推荐
vue3背景下,el-input嵌套在弹出框中,自动聚焦“失效”?如何实现自动聚焦_vue3 el-input 自动聚焦autofocus无效-程序员宅基地
文章浏览阅读436次,点赞15次,收藏2次。原因或许是,使用autofocus时,确实聚焦了!但是当我们又点击 显示弹出框的按钮时,input又失焦了,所以当我们看到input框时,没有自动聚焦。_vue3 el-input 自动聚焦autofocus无效
linux网络服务配置说课,《说课稿LINUX》PPT课件.ppt-程序员宅基地
文章浏览阅读222次。《《说课稿LINUX》PPT课件.ppt》由会员分享,可在线阅读,更多相关《《说课稿LINUX》PPT课件.ppt(16页珍藏版)》请在装配图网上搜索。1、LINUX 基础应用与配置管理 桂林山水职业学院计算机系 朱笑雷 主要内容 课程定位 1 课程内容设置 2 教学方法与手段 3 教材建设 4 教学团度 5 主要内容 实践条件 6 课程考核 7 教学效果 8 课程特色 9 建设思路 10 一、课..._linux说课课件
在SpringBoot中启动时关于连接数据库失败的问题_springboot启动时数据库连接失败 不关闭-程序员宅基地
文章浏览阅读2.2k次。#在SpringBoot中启动时关于连接数据库失败的问题对照了application.yml,发现配置文件貌似没什么问题,但是在查找信息之后,发现问题正是出现在application.yml中问题出于datasource下的data-username和data-password只要将data-username和data-password改为username和password即可..._springboot启动时数据库连接失败 不关闭
antd-pro(V5)动态菜单_antdpro的菜单-程序员宅基地
文章浏览阅读4.6k次。一般情况下登录系统后菜单是由后端返回的,不是前端写死的。antd-pro也支持,修改的路径在app.tsx在 layout 里加一个menuDataRender字段先给一个() =>[]可以看到左侧菜单没了,说明配置生效了,接下来就可以围绕这个配置做文章了,我们先定义一个 menuDataRender方法。根据登录缓存到本地的数据做下处理,判断菜单里要展示哪些内容(比如替换字段,隐藏不显示的菜单,隐藏按钮等),处理好了后返回一个数组结构即可。示例代码如下export const layout: _antdpro的菜单
Linux安装使用jprofiler6分析服务器应用状态-程序员宅基地
文章浏览阅读77次。为什么80%的码农都做不了架构师?>>> ..._jprofiler6 key
苏小红C语言第四版课后习题练习7.7最大公约数三种计算方式_c语言程序设计第四版课后题答案苏小红第七章-程序员宅基地
文章浏览阅读170次。(可以看出递归算法更加侧重于计算的技巧,并且计算机计算的次数也相对更少);_c语言程序设计第四版课后题答案苏小红第七章
随便推点
Fiddler抓包,并修改请求数据_filder改数据包-程序员宅基地
文章浏览阅读4.4w次,点赞8次,收藏51次。浏览器抓包(工具:fiddler)并 修改请求内容 工具下载:https://pan.baidu.com/s/1pyKdAwgTdNNvoWA2bGlk9A 1、正常打开网页,输入要提交的内容 2、打开工具,f11暂停了页面的所有提交动作 3、这时再点击提交按钮,请求的数据就会被工具拦截 4、双击截取的数据,右侧会看到请求的具体内容,任意修改数据 5、点击绿色按钮 run ..._filder改数据包
视频格式转换器榜单:10 款最值得拥有的高清视频转换器_奇客视频转换-程序员宅基地
文章浏览阅读560次。如果您想在计算机或任何其他设备上播放高质量的视频,高清视频转换器可以帮助确保您的视频与您的操作系统和硬件兼容。您还可以使用高清转换器更改视频的分辨率,无论您是想提高质量还是降低分辨率以生成更小的文件。在下表中,我们描述了用于转换高清视频的最流行和可用的桌面程序和在线服务。它们各有优缺点,因此请根据您的需要进行选择。_奇客视频转换
Unity血条效果,图片动画_游戏血条动图-程序员宅基地
文章浏览阅读1.9k次。欢迎来到unity学习、unity培训、unity企业培训教育专区,这里有很多U3D资源、U3D培训视频,我们致力于打造业内unity3d培训、学习第一品牌。今天开始做我们的游戏了,组长给分配了任务,我负责做剧情动画,人物血条和种植植物。 一、剧情动画 动画是以多个图片的形式展现的,图片是自己制作的。 private GUITextu_游戏血条动图
环境变量的加载顺序、环境变量集合_环境变量的顺序-程序员宅基地
文章浏览阅读1k次。*******字符编码ASCII,GB2312,GBK,Unicode,UTF-8比较参考:https://blog.csdn.net/softwarenb/article/details/51994943**环境变量的加载顺序:Mac系统的环境变量,加载顺序为:a. /etc/profileb. /etc/pathsc. ~/.bash_profiled. ~/..._环境变量的顺序
科学家发现让人类幸福感飙升的密码!给大脑植入这个算法 | 精选-程序员宅基地
文章浏览阅读316次。▼大型年度AI人物评选——2017中国AI英雄风云榜已于12月4日在乌镇张榜,12月18日在北京国贸三期举行颁奖典礼。榜单评选出年度技术创新人物TOP 10;商业创新人物TOP 10,获取完整榜单请关注网易智能公众号(ID:smartman163),回复关键词“评奖”。本文系网易智能工作室出品聚焦AI,读懂下一个大时代【网易智能讯12月10日消息】不只有你会_人类大脑植入代码
正则表达式匹配中括号内的内容_正则<>里内容-程序员宅基地
文章浏览阅读3.6k次。几经研究, 终于实现了。time[2020-06-04 11:43:36](?<=\[)(.*)(?=])(pattern) 匹配 pattern 并获取这一匹配。所获取的匹配可以从产生的 Matches 集合得到,在VBScript 中使用 SubMatches 集合,在JScript 中则使用 $0…$9 属性。要匹配圆括号字符,请使用 '\(' 或 '\)'。 (?:pattern) 匹配 pattern 但不获取匹配结..._正则<>里内容